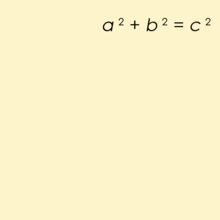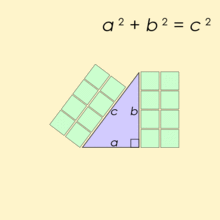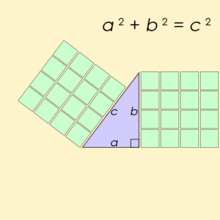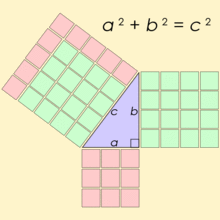Find all the pythagorean triplets in an array of integer

    1) First sort the array, then square each number, now for every element   
       a\[i\] in the array find if a pair exist with sum as a\[i\], this can be   
       done in O(n) space and O(nlog n) for sorting  
    2) start for last index of square array.  
    3) Find 2 elements in square array form beginning to that element, which adds up to it.   
        For doing it in O(n), use solution given in [previous post](http://k2code.blogspot.in/2012/01/given-integer-array-and-number-x-find.html).   
        Here our array becomes, a\[left+1\] to a\[right-1\], and sum becomes a\[left\]+a\[right\].  

FindTriplets(int\[\] A)  
{    //Find triplets in an integer array which satisfy a\[i\]^2 + a\[j\]^2 = a\[k\]^2    
        
    A\[\] = 2 1 9 4 8 7 6 3 5 //input          
    Sort(A); // Sort the input array          
    //Finally A\[\] = 1 2 3 4 5 6 7 8 9          
    //Make an array of squares to avoid compute them again and again   
 int\[\] Sq = new int\[A.length\];  
    for (i=0; i < n; i++)    
    {    
  Sq\[i\] = A\[i\]\*A\[i\];    
    }    
    //Finally Sq\[\] =1 4 9 16 25 49 64 81    
        
    n = length;    
    for (i=n; i > 0; i--)    
    {    
  bool res = TwoSum( B(i...n-i),A\[i\],A\[n-i\])  
 if (res)    
    {    
  print(triplet);    
    }    
  //Search for 2 numbers in Sq array from 0 to i-1 which    
  //adds to Sq\[i\] like we have discussed in last post.    
  //This will give u a search result in O(n) time.    
  //Make res as true if we are able to find any triplet.    
        
  
}    
  
public bool TwoSum(int\[\] B, int a,int b)  
{  
 //return if (a+b) exists in B\[\]  
}